Efficient Globally Optimal 2D-to-3D Deformable Shape Matching
Authored by Zorah Lähner, Emanuele Rodolà, Frank R. Schmidt, Michael M. Bronstein, Daniel Cremers
Published in Conference on Computer Vision and Pattern Recognition (CVPR) 2016
Abstract
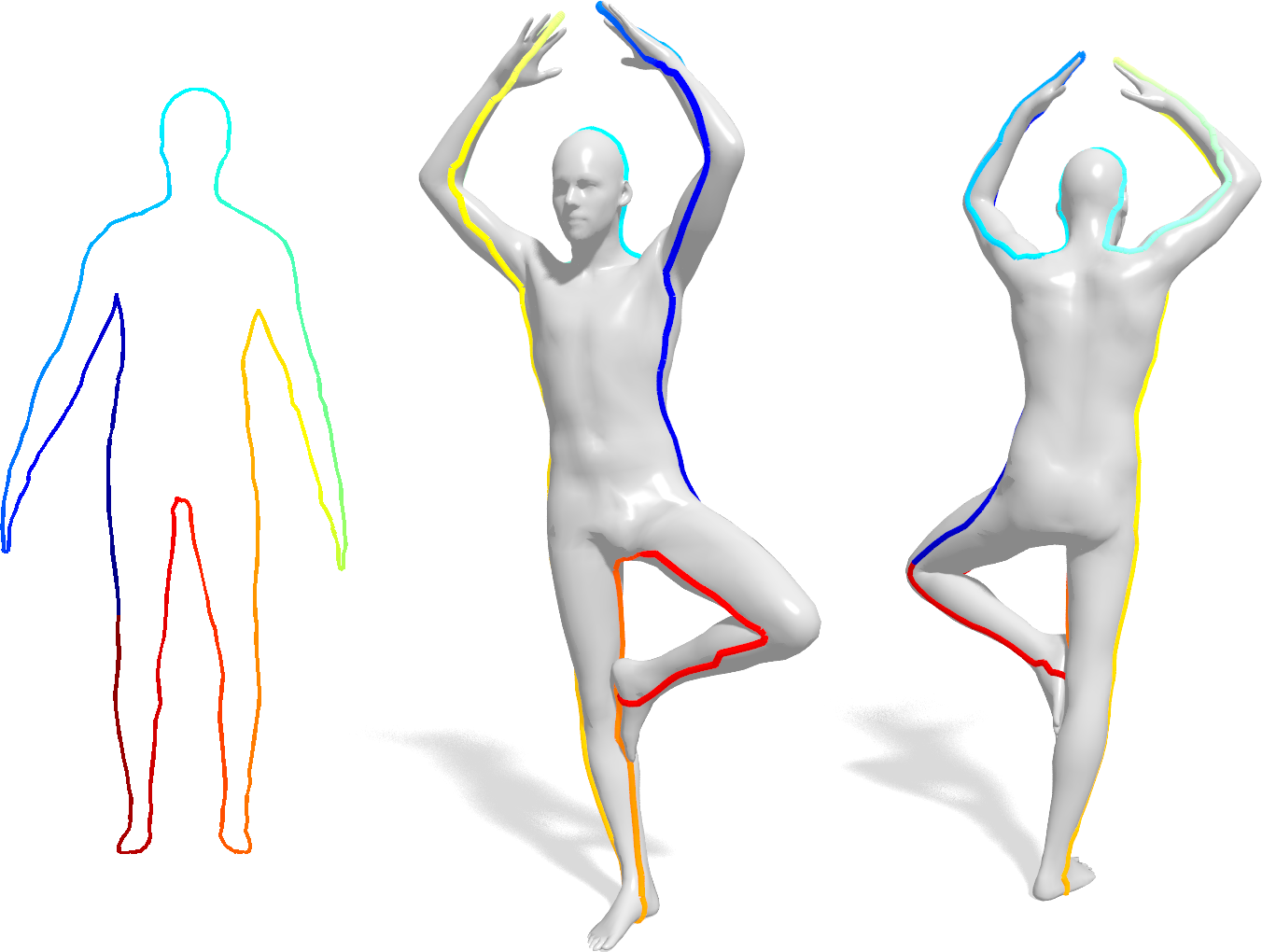
We propose the first algorithm for non-rigid 2D-to-3D shape matching, where the input is a 2D query shape as well as a 3D target shape and the output is a continuous matching curve represented as a closed contour on the 3D shape. We cast the problem as finding the shortest circular path on the product 3-manifold of the two shapes. We prove that the optimal matching can be computed in polynomial time with a (worst-case) complexity of O(mn^2 log(n)), where m and n denote the number of vertices on the 2D and the 3D shape respectively. Quantitative evaluation confirms that the method provides excellent results for sketch-based deformable 3D shape retrieval.
Resources
Data
(dataset parameter tuning, 2.7GB) based on MPI FAUST
(dataset retrieval, 2.9GB) based on TOSCA high-res
Additional Code
(matching code, 281MB) Matlab/C++ Code, example with precomputed data reproducing one matching
(retrieval code, 270kB) Matlab Code, code outline to run retrieval on a new data set, needs matching code
Bibtex
@inproceedings{ laehner2016elastic2D3D,
author = { Zorah Lähner and Emanuele Rodolà and Frank R. Schmidt and Michael M. Bronstein and Daniel Cremers },
title = { Efficient Globally Optimal 2D-to-3D Deformable Shape Matching },
booktitle = { Conference on Computer Vision and Pattern Recognition (CVPR) },
year = { 2016 },
}